P(A|B) = (P(B|A)P(A))/P(B)
De acuerdo, no es la manera más común ni, por supuesto, la más clara de empezar un artículo pero resulta que es de eso que vamos a hablar, algo que, como dice el título, tiene que ver con conocimiento y con milagros.
Se trata del teorema de Bayes y, aunque muchos de nosotros no hemos oído hablar de él, las estadísticas bayesianas han permeado todo, desde la física -con interpretaciones bayesianas de la mecánica cuántica y defensas bayesianas de las teorías de cuerdas y multiverso- hasta la investigación del cáncer y el covid, pasando por la ecología, la filosofía, la neurología, la psicología, además de la informática.
Hay hasta científicos cognitivos que han conjeturado que nuestros cerebros incorporan algoritmos bayesianos al percibir, deliberar y decidir, y fanáticos del teorema que señalan que si adoptáramos el razonamiento bayesiano consciente (más allá del procesamiento bayesiano inconsciente que supuestamente emplea nuestro cerebro), el mundo sería mejor.
Ante todo eso, vale la pena saber un poco sobre esa fórmula con la que empezamos y su autor.
Él
"Thomas Bayes fue un ministro presbiteriano en el siglo XVIII", empezó contándole a la BBC Sharon Bertsch McGrayne, autora del libro "La teoría que nunca murió".
De Bayes no hay retratos, pero tenemos su firma.
"Fue parte de una generación que no pudo asistir a la universidad en Oxford o Cambridge, las principales universidades inglesas en ese momento, porque no era la Iglesia de Inglaterra.
"Esto fue una suerte para Bayes porque se fue al norte a Escocia, que era presbiteriana y tenía una universidad mucho mejor en Edimburgo en ese momento, y allí estudió teología, como su padre, y matemáticas, que era su verdadero interés, y se convirtió en un matemático aficionado".
Bayes logró mezclar sus dos intereses, escribió al menos un libro sobre matemáticas y pasó gran parte de su tiempo estudiando las obras de otros matemáticos y teólogos.
Así, comenzó a desarrollar una idea.
La idea
"Fue durante una gran controversia religiosa de si se podía usar la evidencia del mundo natural para demostrar que Dios existe".
Uno de los que participó en el debate fue el filósofo David Hume quien publicó, en 1748, el hasta hoy influyente libro "Investigación sobre el entendimiento humano", cuestionando, entre otras cosas, la existencia de milagros.
David Hume, 1711-1776. Historidor y filósofo, pintado por Allan Ramsay en 1754.
Según Hume, la probabilidad de que las personas afirmaran incorrectamente que habían visto la resurrección de Jesús superaba con creces la probabilidad de que el evento hubiera ocurrido en primer lugar.
"Un milagro es una violación de las leyes de la naturaleza; y como una experiencia firme e inalterable ha establecido estas leyes, la prueba contra un milagro, por la naturaleza misma del hecho, es tan completa como se pueda imaginar que cualquier argumento basado en la experiencia lo sea", escribió el filósofo.
Esto no le cayó bien al reverendo y, queriendo demostrar que Hume estaba equivocado, empezó a tratar de cuantificar la probabilidad de un evento imaginándose situaciones como la siguiente:
Imagínate que estás en una habitación y a tus espaldas está una mesa.
Alguien lanza una pelota que aterriza en esa mesa pero, sin mirar, no tienes forma de saber dónde.
Entonces, le pides a esa persona que lance otra pelota y te diga si cayó a la derecha o a la izquierda de la primera. Si aterrizó hacia la derecha es más probable que la primera esté en el lado izquierdo de la mesa, pues supones que hay más espacio a ese lado para que caiga la segunda bola.
Con cada nueva pelota que se lance, puedes actualizar tu conjetura e ir precisando la ubicación de la original.
De manera similar, pensó Bayes, los diversos testimonios de la resurrección de Cristo indicaban que el evento no podía descartarse de la forma en que Hume afirmó.
"La resurrección", pintada circa 1475, por el artista español Bartolomé Bermejo (ca 1440-ca 1498).
"Se le ocurrió un teorema de una línea realmente simple que sirve para trabajar con datos incompletos y dijo que está bien comenzar con una idea a medias sobre una situación, siempre y cuando modifiques implacablemente tus ideas iniciales cada vez que aparezca nueva información", señaló McGrayne.
"Nos dio un razonamiento matemático para situaciones altamente inciertas".
El rechazo
Bayes no publicó su teorema pero un amigo suyo, Richard Price, un matemático aficionado, lo desarrolló y, en 1767, publicó "Sobre la importancia del cristianismo, sus evidencias y las objeciones que se le han hecho", en el que usó las ideas de Bayes para desafiar el argumento de Hume.
"El punto probabilístico básico" de Price, dice el historiador y estadístico Stephen Stigler en su artículo "El verdadero título del ensayo de Bayer", "fue que Hume subestimó el impacto de que hubiera varios testigos independientes de un milagro, y que los resultados de Bayes mostraron cómo la multiplicación de incluso evidencia falible podría abrumar la gran improbabilidad de un evento y establecerlo como un hecho".
Quizás ni siquiera así Price logró probar la existencia de los milagros, pero sí sacó a la luz pública algo que de otra forma se habría quedado oculto entre los papeles del para entonces ya difunto Bayes.
No obstante, el teorema cayó en la oscuridad hasta que el ilustre matemático francés Pierre Simon Laplace formalizó la visión de Bayes y mostró claramente cómo se podía aplicar a principios del siglo XIX.
Pierre-Simon Laplace (Beaumont-en-Auge, 1749-París, 1827), marqués de Laplace, matemático y astrónomo francés, fue quien le dio prominencia al trabajo de Bayes.
A partir de entonces, entró y pasó de moda, se aplicó en una ciencia tras otra sólo para luego ser condenado por ser vago, subjetivo o poco científico, y se convirtió en la manzana de la discordia entre campos rivales de matemáticos antes de disfrutar de un renacimiento en los últimos años.
¿Por qué?
Recuerda que el enfoque bayesiano dice que puedes comenzar con una estimación subjetiva de una probabilidad, cualquier probabilidad, independientemente de si hay algún dato.
¿Cuán probable es que Dios exista? ¿Mutará el nuevo coronavirus para inutilizar las vacunas? ¿Cuál es la posibilidad de una guerra nuclear antes del 1 de enero de 2030?
Habiendo comenzado con lo que es poco más que una suposición, usamos la regla de Bayes para revisar nuestra opinión a medida que llegan nuevos datos.
John Stuart Mill, el filósofo y economista político británico del siglo XIX, lo llamó "la ignorancia acuñada en la ciencia".
Durante mucho tiempo, el enfoque bayesiano fue tabú en las estadísticas convencionales, pero no murió, y a lo largo de las décadas personas inteligentes encontraron formas inteligentes de aplicarlo.
Enigma
Un caso sorprendente es que el teorema de Bayes fue utilizado por Alan Turing mientras trabajaba con su equipo descifrando el código Enigma utilizado por los submarinos alemanes o los U-Boot durante la Segunda Guerra Mundial.
El teorema de Bayes le sirvió a Turing para salvar a millones de personas.
"En ese momento, los submarinos salían de Francia y recibían órdenes de radio de dónde ir y qué hacer, y esas órdenes eran un lenguaje codificado llamado Enigma. Y la Armada alemana lo había hecho tan complicado que nadie en Reino Unido ni en Alemania pensó que los británicos podrían descifrarlo", recuerda McGrayne.
Pero Turing estaba decidido a hacerlo, aprovechando cuanto pudieran.
"Conocían la organización general de una oración alemana. Se dieron cuenta de que usaban la palabra eins (1 en alemán) en casi todos los mensajes, así que allí tenían tres letras. Esa fue una pista. Así siguieron agregando datos una y otra y otra vez".
Turing y sus colegas crearon un sistema bayesiano para adivinar un tramo de letras en un mensaje Enigma, medir su creencia en la validez de estas conjeturas utilizando métodos bayesianos para evaluar las probabilidades y agregar más pistas a medida que llegaban.
"Eventualmente pudieron leer los mensajes".
Cuando los hechos cambian...
Así, fue utilizado por muchas otras personas y una vez que llegaron las computadoras, sencillamente explotó.
Para darte una idea de cómo funciona, responde esta pregunta: Si obtienes un resultado positivo en una prueba de covid que solo da un falso positivo una vez de cada 1.000, ¿cuál es la probabilidad de que realmente tengas coronavirus?
¿Pensaste que el 99,9%?... La respuesta correcta es que no tienes suficiente información para saberlo.
Es ahí cuando entra en juego el teorema de Bayes. Su notación matemática, esa que está al principio del artículo, parece complicada. Pero es más fácil de entender con un ejemplo que decifrando el significado de todos esos símbolos.
Imagínate que te sometes a una prueba para detectar una enfermedad. La prueba es increíblemente precisa: si la persona tiene la enfermedad, lo dirá correctamente el 99% de las veces; si no, también. Pero la enfermedad en cuestión es muy rara; sólo una persona de cada 10.000 la tiene. Esto se conoce como su "probabilidad previa": la tasa de fondo en la población.
Así que ahora imagina que le hacen la prueba a 1'000.000 de personas. Hay 100 personas que tienen la enfermedad: la prueba identifica correctamente a 99 de ellas. Y hay 999.900 personas que no la tienen: la prueba identifica correctamente a 989,901 de ellas.
Pero eso significa que la prueba, a pesar de dar la respuesta correcta en el 99% de los casos, le ha dicho a 9.999 personas que tienen la enfermedad, cuando en realidad no es así.
Entonces, si obtienes un resultado positivo, en este caso, tu probabilidad de tener la enfermedad es de 99 en 10.098, o poco menos del 1%. Sin el enfoque bayensiano se asustaría a muchas personas y se las enviaría a procedimientos médicos intrusivos y potencialmente peligrosos por un diagnóstico erróneo.
Sin conocer la probabilidad previa, no se sabe cuán probable es que un resultado sea falso o verdadero.
"Según Bill Gates, la base del éxito de Microsoft fue el uso de Bayes", cuenta McGrayne.
Este no es un problema hipotético.
En medicina, por ejemplo, una revisión de casos realizada en 2016 encontró que el 60% de las mujeres que se hicieron mamografías anuales durante 10 años tuvieron al menos un falso positivo. En los tribunales de justicia, una falla conocida como la "falacia del fiscal", que puede condenar a inocentes, también depende del teorema.
Y eso es sólo la punta del iceberg. Los investigadores utilizan la estadística bayesiana para abordar problemas de formidable complejidad.
El razonamiento bayesiano combinado con la potencia informática avanzada ha revolucionado la búsqueda de planetas que orbitan estrellas distantes; las estadísticas bayesianas contribuyeron a la reducción de la edad del Universo, que a fines de la década de 1990 se calculaba entre 8.000 a 15.000 millones de años y ahora se ha concluido con cierta confianza que es de 13.800 millones de años.
"Hoy en día se utiliza en la genética, para detectar diferencias sutiles en el ADN y las proteínas, así como para proteger la vida silvestre, hacer estudios cerebrales, traducir idiomas extranjeros...", enumera la autora de "La teoría que nunca murió".
"Se ha incrustado en la informática, el aprendizaje automático, la inteligencia artificial.
"Puede que no sea exactamente como lo hizo Bayes, pero se ha modernizado y es increíblemente útil... está en todas partes", señaló McGrayne en conversación con la BBC y concluyó con una cita que se le han atribuido a los economistas John Maynard Keynes y Paul Samuelson, así como al premier británico Winston Churchill y otros, para resumir la esencia del teorema de Bayes:
"Cuando los hechos cambian, yo cambio de opinión. ¿Usted qué hace?".

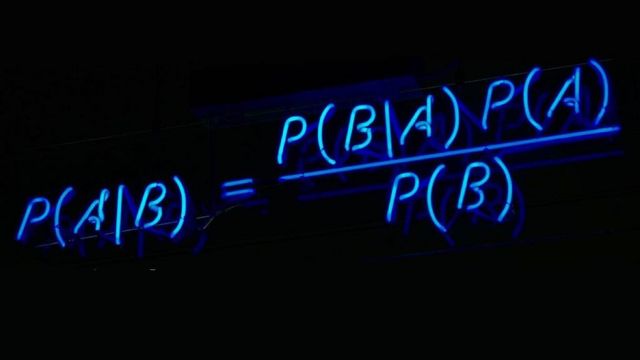








No hay comentarios:
Publicar un comentario