Cómo la lengua configura nuestro pensamiento
En este vídeo, Lera Boroditsky reflexiona sobre su área de estudio, la ciencia cognitiva, y explica alguno de los experimentos en los que trabaja para mostrar el poder que tienen las palabras en el pensamiento. ¿Influye la lengua que hablamos en nuestra manera de interpretar el mundo? ¿Se comportan diferente los bilingües dependiendo de la lengua que estén usando? “Las palabras no están aisladas”, dice Boroditsky, haciendo referencia a que las palabras están unidas a recuerdos y experiencias que nos condicionan.
La científica considera otros temas como el vocabulario, la categorización o las metáforas y su implicación en nuestra percepción de temas socialmente complejos. “El lenguaje es una herramienta mágica que nos diferencia del resto de seres vivos”, sentencia.
Lera Boroditsky es investigadora y profesora en el campo de la ciencia cognitiva. Su trabajo se enfoca en el área del lenguaje y la cognición. Es una de las fundadores de la teoría de la relatividad lingüística. La científica ha desempeñado su carrera en el MIT y en Stanford. Actualmente es profesora asociada de ciencia cognitiva en la Universidad de California, San Diego y editora jefe de Frontiers in Cultural Psychology.
Su investigación se centra en las relaciones entre la mente, el mundo y el lenguaje con un enfoque multidisciplinar que incluye la lingüística, la psicología, la neurociencia o la antropología. En su labor de divulgación científica ha publicado en prestigiosos medios como el Wall Street Journal, Scientific American o The Economist. Lera Boroditsky ha sido nombrada una de los ‘25 Visionarios que están cambiando el mundo’ por el Utne Reader, y ha recibido, además, numerosos galardones como el prestigioso premio ‘NSF Career Award’.
NEUROCIENCIA EN LA EDUCACIÓN
La neurociencia es un campo de conocimiento interdisciplinar que abarca toda una serie de investigaciones sobre el cerebro y los procesos neuronales: desde las estructuras moleculares, pasando por las redes neuronales y el cerebro, hasta la estructura y el funcionamiento del cerebro, y la conexión entre los procesos neuronales y la fisiología general y el comportamiento humano. La neurociencia ha evolucionado más allá de la neurobiología para incluir los métodos de la neurofisiología, la medicina, la farmacología y la genética.
Los estudios de la interconexión del sistema nervioso con diversos aspectos de la actividad humana permitieron incorporar los métodos de la psicología, la lingüística, la informática y las ciencias cognitivas a la neurociencia y llegar a la formación de muchas disciplinas nuevas, como la neuropsicología, la neuroética, la neuroinformática y otras, y crear investigaciones interdisciplinarias.
👉 Métodos de neurociencia
La base de los métodos neurocientíficos es la neuroimagen, es decir, la fijación y visualización directa del funcionamiento de diferentes partes del cerebro y otras partes del sistema nervioso en determinados estados humanos y en la realización de determinadas acciones por parte del ser humano:
- La resonancia magnética (RM) es un método de obtención de imágenes de las partes internas del cerebro mediante resonancia magnética nuclear;
- Resonancia magnética funcional (fMRI): permite determinar la activación de una región específica del cerebro durante su funcionamiento normal bajo la influencia de diversos factores físicos y en diversas condiciones;
- La tomografía por emisión de positrones (PET) es un método tomográfico con radionúclidos para el estudio de órganos internos humanos o animales. El método se basa en el registro de pares de rayos gamma que surgen de la aniquilación de positrones con electrones;
- La magnetoencefalografía (MEG) es una técnica de neuroimagen utilizada para medir, mediante dispositivos especialmente sensibles, los campos magnéticos producidos por la actividad eléctrica del cerebro;
- La electroencefalografía (EEG) es un método de estudio del estado funcional del cerebro mediante el registro de su actividad bioeléctrica;
- Estimulación magnética transcraneal: una tecnología que puede activar o, por el contrario, ralentizar el trabajo de áreas cerebrales individuales;
- El seguimiento ocular, u oculografía, es una tecnología que rastrea los movimientos oculares y permite trazar la secuencia en la que los ojos del observador fijan diferentes partes del objeto en cuestión.
👉 Oportunidades de utilizar diferentes disciplinas de la neurociencia en la enseñanza
| Disciplina | Neurofisiología (neurofisiología) es una rama de la fisiología que estudia la función y la interacción del sistema nervioso y las neuronas | Neurociencia cognitiva La neurociencia cognitiva es una ciencia que estudia la relación entre la actividad del cerebro y otras partes del sistema nervioso y los procesos cognitivos y el comportamiento. La neurociencia cognitiva presta especial atención al estudio de las bases neurales de los procesos de pensamiento | Neurolingüística (neurolingüística) es una disciplina científica que estudia el sistema del lenguaje y los mecanismos del habla del cerebro | |||
| Alcance | Identificar la relación entre los factores fisiológicos y el proceso de aprendizaje | Estudiar la influencia de los factores externos y los presupuestos en los procesos de pensamiento y las decisiones tomadas | Revelar las peculiaridades de la percepción del discurso oral y escrito en el contexto de palabras específicas y sus combinaciones | |||
| Ejemplo | Los experimentos confirmaron una elevada neuroplasticidad del cerebro en las personas mayores, que compensa algunos cambios cerebrales relacionados con la edad y les permite resolver tareas complejas con más éxito que los sujetos más jóvenes | Según el premio Nobel Daniel Kahneman, los seres humanos dependen de un número limitado de heurísticos que simplifican las complejas tareas de estimación de probabilidades y predicción de valores en operaciones de juicio más simples (superficiales) | El rastreador de la mirada y la tomografía magnética investigan cómo las personas leen textos o ven vídeos, a qué prestan atención en primer lugar y qué regiones del cerebro son responsables de la percepción, el reconocimiento y la conciencia de las palabras y las imágenes |
Impacto del aula invertida en un curso de matemáticas
Por Rafael Benítez Medina y Jesús Grajeda Rosas
“Aula invertida es la metodología pedagógica que mejor se adapta a la “nueva normalidad educativa”.
La pandemia provocada por el COVID-19 ha situado a las tecnologías digitales como parte esencial de los procesos de enseñanza y aprendizaje. Millones de estudiantes pasaron repentinamente de un entorno de aprendizaje presencial a uno virtual. Ante la inminente llegada de la “nueva normalidad educativa” la educación virtual será una de las estrategias que garanticen la continuidad de los programas académicos en las instituciones educativas. El aula invertida es una metodología de aprendizaje que se caracteriza por potencializar los espacios virtuales de aprendizaje, por lo tanto, es una de las metodologías que mejor se adapta a esta “nueva normalidad educativa”.
El aula invertida es una estrategia que invierte el entorno de aprendizaje tradicional. Los contenidos del curso se aprenden fuera del aula, mientras las tareas o actividades son implementadas durante la clase de manera colaborativa. Los estudiantes reciben los contenidos teóricos del curso a través de videos diseñados o supervisados por el profesor, permitiendo que durante la clase el profesor pueda implementar actividades de aprendizaje significativo y profundizar en los contenidos del curso.
Es muy común que al realizar una búsqueda en Internet revisemos el primer video que nos arroja la consulta. Esto mismo hacen los alumnos. Pero, ¿cómo pueden saber que lo que aparece en ese video es correcto? ¿De qué forma se aseguran de que sea justo lo que el profesor busca que aprendan? Ante esta problemática es necesario que el profesor supervise los videos que consultarán los alumnos como contenidos de la clase o cree materiales específicos para su curso donde aborde ejemplos contextualizados con un lenguaje apropiado a la formación profesional. En este artículo queremos evidenciar la utilidad que tiene para los alumnos que los temarios de matemáticas incluyan ligas de videos creados por los propios maestros.
“El uso de videos creados por los profesores y el método de aula invertida tienen un impacto favorable en los resultados de aprendizaje y el rendimiento de los estudiantes”.
Es importante recordar que el video es uno de los principales recursos en aula invertida, pero también se pueden utilizar otros recursos electrónicos como la función “compartir pantalla” de la aplicación Zoom, la metodología Storytelling, simulaciones, libros electrónicos y revistas electrónicas, entre otros.
En este artículo pretendemos fortalecer las investigaciones realizadas por Baki (2016), Barros & Martínez (2018), Jordán, Pérez, & Sanabria (2014); en las que se contrasta el rendimiento de los estudiantes cuando llevan un curso de forma tradicional con el rendimiento que logran los estudiantes mediante aula invertida.
A continuación, presentamos el trabajo de investigación que realizamos en un curso de matemáticas II para alumnos de licenciatura del Tecnológico de Monterrey.
Creación de material audiovisual. Creamos videos suficientes para cubrir todo el curso. Para ello, utilizamos criterios como la redacción de los problemas, la definición de variables y la aplicación del problema, considerados en Grajeda & Benítez (2018). Los videos completos se pueden consultar en el canal de YouTube Matemáticas con Grajeda.
Implementación del aula invertida en un grupo experimental. Los videos creados se utilizaron en el grupo experimental con la técnica de aula invertida. Todas las sesiones fueron muy similares. Les pedimos a los alumnos que en casa consultaran el video del tema de la siguiente clase, tomaran notas, hicieran un resumen o resolvieran los ejercicios que ahí se explicaban. En clase atendimos dudas sobre los videos y resolvimos ejercicios complementarios con los alumnos en el pizarrón. El tiempo restante de la clase era para que los alumnos practicaran lo aprendido y profundizaran en los temas.
Contraste entre el aprovechamiento del grupo experimental frente al grupo de control. En diferentes momentos del curso medimos el desempeño de los alumnos en el grupo experimental y lo contrastamos con el desempeño del grupo de control. En ambos grupos el desempeño de los alumnos se midió a través de un examen de conocimientos, el rango de este examen fue de 0 a 100 y la calificación mínima aprobatoria de 70.
En un primer análisis usamos la mediana para interpretar los resultados. La imagen 1 muestra que la mediana del grupo experimental es mayor que la del grupo de control en las primeras cinco evaluaciones. Esto significa que el 50 % de las mejores calificaciones obtenidas por los estudiantes en el grupo experimental son mejores que el 50 % de las mejores calificaciones obtenidas por los estudiantes en el grupo de control.
Estos resultados son evidencia de que utilizar videos creados por los propios profesores para cubrir los contenidos disciplinarios del curso de matemáticas tiene un impacto favorable en el aprendizaje de los estudiantes.
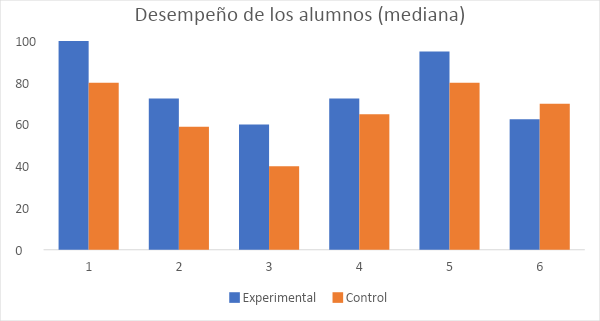
Imagen 1. Valor mediano de los alumnos en las evaluaciones del curso.
Si observamos bien los resultados de la evaluación número seis (que es el examen final), no son consistentes con los resultados de las cinco evaluaciones del curso anteriores. ¿Cómo explicar este resultado? Es difícil probarlo, pero pensamos que se debe a comportamientos actitudinales de los alumnos. El examen final es una evaluación que se aplica una semana después de finalizar el curso y corresponde al 20 % de la calificación final, para este momento, el 39 % de los alumnos del grupo experimental llegaron aprobados al examen final mientras que en el grupo de control tan solo del 21 %. El resto de los alumnos puede hacer una estimación de lo que necesita obtener en el examen final para aprobar el curso. Esto produce un cierto relajamiento o desconcentración en aquellos alumnos que han obtenido buenas calificaciones durante el curso y una concentración o esfuerzo adicional en aquellos alumnos que no han obtenido buenas calificaciones y están obligados a realizar un buen examen final para poder aprobar el curso.
Consideramos que estas actitudes de relajamiento y concentración se reflejan en las evaluaciones del examen final y en cierta medida pueden explicar porque se invierten los resultados obtenidos en el grupo de control y el grupo tradicional.
La imagen 2 muestra un segundo análisis referente al rendimiento promedio de los alumnos. A excepción de la evaluación final, que como ya se mencionó anteriormente, tiene algunos aspectos actitudinales de los alumnos difíciles de medir; los alumnos del grupo experimental parecen tener un mejor rendimiento promedio que los alumnos del grupo de control.
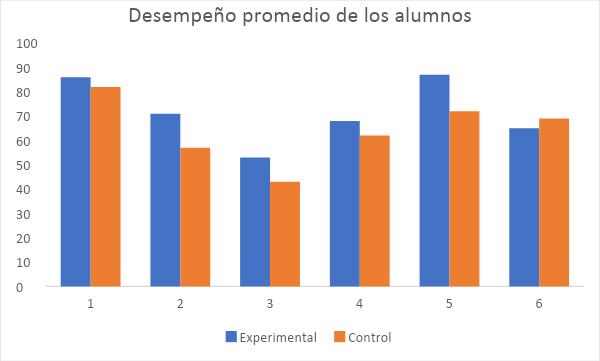
Imagen 2. Desempeño promedio de los alumnos en las evaluaciones del curso.
A partir de estos resultados y análisis, podemos mostrar que el uso de videos creados por los profesores y el método de aula invertida tienen un impacto favorable en los resultados de aprendizaje y el rendimiento de los estudiantes.
La implementación de metodologías para el aprendizaje innovadoras y el uso de la tecnología, permite a los profesores diseñar soluciones para enriquecer el proceso de aprendizaje de nuestros alumnos. Los invitamos a explorar estas opciones en su práctica docente y a compartir sus resultados con el Observatorio de Innovación Educativa.
Acerca de los autores
Rafael Benítez Medina (rafael.benitez@tec.mx) es Licenciado en Física y Matemáticas con una Maestría en Matemáticas. Actualmente es profesor de planta del Instituto Tecnológico y de Estudios Superiores de Monterrey, campus Santa Fe, el profesor Benítez ha participado como ponente en diversos congresos nacionales e internacionales de innovación educativa, cuenta con un artículo de investigación en el área de matemáticas y varias publicaciones de innovación educativa.
Jesús Grajeda Rosas (mc.jesusgr@tec.mx) es Maestro en Ciencias con especialidad en Matemática Educativa. Profesor de cátedra en el Instituto Tecnológico y de Estudios Superiores de Monterrey, Campus Santa Fe. Ha impartido ponencias a nivel nacional e internacional.
Referencias
Baki K. (2016). The effect of using flipped classroom instruction on student’s achievement in the new 2016 scholastic assessment test mathematics skills in the United Arab Emirates (Master Thesis). United Arab Emirates University, United Arab Emirates
Barros V. y Martínez M. (2018). Aula invertida en la enseñanza del álgebra en la educación superior. Espirales. Revista interdisciplinaria de investigación. 2(13). 12-23.
Jordán C., Pérez M. y Sanabria E. (2014). Investigación del impacto en un aula de matemáticas al utilizar flip educación. Revista. Pensamiento matemático, 4(2). 9-22.
Grajeda J., Benítez R y Morales S. (2018). Reflexiones sobre el efecto del uso de videos direccionados en cursos de matemáticas para licenciatura en el Tecnológico de Monterrey. Memorias del Congreso Internacional de Innovación Educativa, 1652-1656.
Matemáticas con Grajeda. Recuperado el 27 de abril de 2020 de https://www.youtube.com/channel/UCX-9il8XGlV6kkrIVyTdWQQ
Reporte EduTrends (2014). Aprendizaje invertido. Observatorio de Innovación Educativa del Tecnológico de Monterrey.
Qué es el teorema de Bayes, el potente método para generar conocimiento que nació cuando trataban de demostrar un milagro
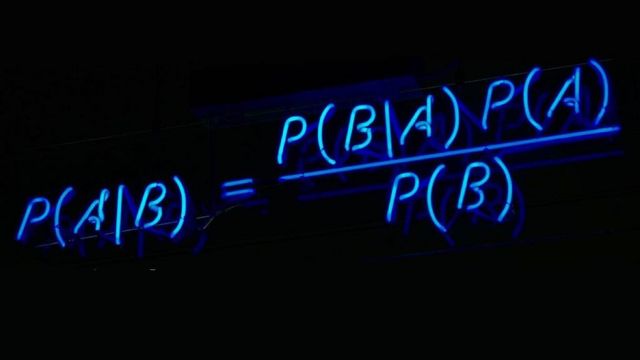
FUENTE DE LA IMAGEN,MATTBUCK
P(A|B) = (P(B|A)P(A))/P(B)
De acuerdo, no es la manera más común ni, por supuesto, la más clara de empezar un artículo pero resulta que es de eso que vamos a hablar, algo que, como dice el título, tiene que ver con conocimiento y con milagros.
Se trata del teorema de Bayes y, aunque muchos de nosotros no hemos oído hablar de él, las estadísticas bayesianas han permeado todo, desde la física -con interpretaciones bayesianas de la mecánica cuántica y defensas bayesianas de las teorías de cuerdas y multiverso- hasta la investigación del cáncer y el covid, pasando por la ecología, la filosofía, la neurología, la psicología, además de la informática.
Hay hasta científicos cognitivos que han conjeturado que nuestros cerebros incorporan algoritmos bayesianos al percibir, deliberar y decidir, y fanáticos del teorema que señalan que si adoptáramos el razonamiento bayesiano consciente (más allá del procesamiento bayesiano inconsciente que supuestamente emplea nuestro cerebro), el mundo sería mejor.
Ante todo eso, vale la pena saber un poco sobre esa fórmula con la que empezamos y su autor.
Él
"Thomas Bayes fue un ministro presbiteriano en el siglo XVIII", empezó contándole a la BBC Sharon Bertsch McGrayne, autora del libro "La teoría que nunca murió".

De Bayes no hay retratos, pero tenemos su firma.
"Fue parte de una generación que no pudo asistir a la universidad en Oxford o Cambridge, las principales universidades inglesas en ese momento, porque no era la Iglesia de Inglaterra.
"Esto fue una suerte para Bayes porque se fue al norte a Escocia, que era presbiteriana y tenía una universidad mucho mejor en Edimburgo en ese momento, y allí estudió teología, como su padre, y matemáticas, que era su verdadero interés, y se convirtió en un matemático aficionado".
Bayes logró mezclar sus dos intereses, escribió al menos un libro sobre matemáticas y pasó gran parte de su tiempo estudiando las obras de otros matemáticos y teólogos.
Así, comenzó a desarrollar una idea.
La idea
"Fue durante una gran controversia religiosa de si se podía usar la evidencia del mundo natural para demostrar que Dios existe".
Uno de los que participó en el debate fue el filósofo David Hume quien publicó, en 1748, el hasta hoy influyente libro "Investigación sobre el entendimiento humano", cuestionando, entre otras cosas, la existencia de milagros.

FUENTE DE LA IMAGEN,GETTY IMAGES
David Hume, 1711-1776. Historidor y filósofo, pintado por Allan Ramsay en 1754.
Según Hume, la probabilidad de que las personas afirmaran incorrectamente que habían visto la resurrección de Jesús superaba con creces la probabilidad de que el evento hubiera ocurrido en primer lugar.
"Un milagro es una violación de las leyes de la naturaleza; y como una experiencia firme e inalterable ha establecido estas leyes, la prueba contra un milagro, por la naturaleza misma del hecho, es tan completa como se pueda imaginar que cualquier argumento basado en la experiencia lo sea", escribió el filósofo.
Esto no le cayó bien al reverendo y, queriendo demostrar que Hume estaba equivocado, empezó a tratar de cuantificar la probabilidad de un evento imaginándose situaciones como la siguiente:
Imagínate que estás en una habitación y a tus espaldas está una mesa.
Alguien lanza una pelota que aterriza en esa mesa pero, sin mirar, no tienes forma de saber dónde.
Entonces, le pides a esa persona que lance otra pelota y te diga si cayó a la derecha o a la izquierda de la primera. Si aterrizó hacia la derecha es más probable que la primera esté en el lado izquierdo de la mesa, pues supones que hay más espacio a ese lado para que caiga la segunda bola.
Con cada nueva pelota que se lance, puedes actualizar tu conjetura e ir precisando la ubicación de la original.
De manera similar, pensó Bayes, los diversos testimonios de la resurrección de Cristo indicaban que el evento no podía descartarse de la forma en que Hume afirmó.

FUENTE DE LA IMAGEN,GETTY IMAGES
"La resurrección", pintada circa 1475, por el artista español Bartolomé Bermejo (ca 1440-ca 1498).
"Se le ocurrió un teorema de una línea realmente simple que sirve para trabajar con datos incompletos y dijo que está bien comenzar con una idea a medias sobre una situación, siempre y cuando modifiques implacablemente tus ideas iniciales cada vez que aparezca nueva información", señaló McGrayne.
"Nos dio un razonamiento matemático para situaciones altamente inciertas".
El rechazo
Bayes no publicó su teorema pero un amigo suyo, Richard Price, un matemático aficionado, lo desarrolló y, en 1767, publicó "Sobre la importancia del cristianismo, sus evidencias y las objeciones que se le han hecho", en el que usó las ideas de Bayes para desafiar el argumento de Hume.
"El punto probabilístico básico" de Price, dice el historiador y estadístico Stephen Stigler en su artículo "El verdadero título del ensayo de Bayer", "fue que Hume subestimó el impacto de que hubiera varios testigos independientes de un milagro, y que los resultados de Bayes mostraron cómo la multiplicación de incluso evidencia falible podría abrumar la gran improbabilidad de un evento y establecerlo como un hecho".
Quizás ni siquiera así Price logró probar la existencia de los milagros, pero sí sacó a la luz pública algo que de otra forma se habría quedado oculto entre los papeles del para entonces ya difunto Bayes.
No obstante, el teorema cayó en la oscuridad hasta que el ilustre matemático francés Pierre Simon Laplace formalizó la visión de Bayes y mostró claramente cómo se podía aplicar a principios del siglo XIX.

FUENTE DE LA IMAGEN,GETTY IMAGES
Pierre-Simon Laplace (Beaumont-en-Auge, 1749-París, 1827), marqués de Laplace, matemático y astrónomo francés, fue quien le dio prominencia al trabajo de Bayes.
A partir de entonces, entró y pasó de moda, se aplicó en una ciencia tras otra sólo para luego ser condenado por ser vago, subjetivo o poco científico, y se convirtió en la manzana de la discordia entre campos rivales de matemáticos antes de disfrutar de un renacimiento en los últimos años.
¿Por qué?
Recuerda que el enfoque bayesiano dice que puedes comenzar con una estimación subjetiva de una probabilidad, cualquier probabilidad, independientemente de si hay algún dato.
¿Cuán probable es que Dios exista? ¿Mutará el nuevo coronavirus para inutilizar las vacunas? ¿Cuál es la posibilidad de una guerra nuclear antes del 1 de enero de 2030?
Habiendo comenzado con lo que es poco más que una suposición, usamos la regla de Bayes para revisar nuestra opinión a medida que llegan nuevos datos.
John Stuart Mill, el filósofo y economista político británico del siglo XIX, lo llamó "la ignorancia acuñada en la ciencia".
Durante mucho tiempo, el enfoque bayesiano fue tabú en las estadísticas convencionales, pero no murió, y a lo largo de las décadas personas inteligentes encontraron formas inteligentes de aplicarlo.
Enigma
Un caso sorprendente es que el teorema de Bayes fue utilizado por Alan Turing mientras trabajaba con su equipo descifrando el código Enigma utilizado por los submarinos alemanes o los U-Boot durante la Segunda Guerra Mundial.

El teorema de Bayes le sirvió a Turing para salvar a millones de personas.
"En ese momento, los submarinos salían de Francia y recibían órdenes de radio de dónde ir y qué hacer, y esas órdenes eran un lenguaje codificado llamado Enigma. Y la Armada alemana lo había hecho tan complicado que nadie en Reino Unido ni en Alemania pensó que los británicos podrían descifrarlo", recuerda McGrayne.
Pero Turing estaba decidido a hacerlo, aprovechando cuanto pudieran.
"Conocían la organización general de una oración alemana. Se dieron cuenta de que usaban la palabra eins (1 en alemán) en casi todos los mensajes, así que allí tenían tres letras. Esa fue una pista. Así siguieron agregando datos una y otra y otra vez".
Turing y sus colegas crearon un sistema bayesiano para adivinar un tramo de letras en un mensaje Enigma, medir su creencia en la validez de estas conjeturas utilizando métodos bayesianos para evaluar las probabilidades y agregar más pistas a medida que llegaban.
"Eventualmente pudieron leer los mensajes".
Cuando los hechos cambian...
Así, fue utilizado por muchas otras personas y una vez que llegaron las computadoras, sencillamente explotó.
Para darte una idea de cómo funciona, responde esta pregunta: Si obtienes un resultado positivo en una prueba de covid que solo da un falso positivo una vez de cada 1.000, ¿cuál es la probabilidad de que realmente tengas coronavirus?
FUENTE DE LA IMAGEN,SCIENCE PHOTO LIBRARY
¿Pensaste que el 99,9%?... La respuesta correcta es que no tienes suficiente información para saberlo.
Es ahí cuando entra en juego el teorema de Bayes. Su notación matemática, esa que está al principio del artículo, parece complicada. Pero es más fácil de entender con un ejemplo que decifrando el significado de todos esos símbolos.
Imagínate que te sometes a una prueba para detectar una enfermedad. La prueba es increíblemente precisa: si la persona tiene la enfermedad, lo dirá correctamente el 99% de las veces; si no, también. Pero la enfermedad en cuestión es muy rara; sólo una persona de cada 10.000 la tiene. Esto se conoce como su "probabilidad previa": la tasa de fondo en la población.
Así que ahora imagina que le hacen la prueba a 1'000.000 de personas. Hay 100 personas que tienen la enfermedad: la prueba identifica correctamente a 99 de ellas. Y hay 999.900 personas que no la tienen: la prueba identifica correctamente a 989,901 de ellas.
Pero eso significa que la prueba, a pesar de dar la respuesta correcta en el 99% de los casos, le ha dicho a 9.999 personas que tienen la enfermedad, cuando en realidad no es así.
Entonces, si obtienes un resultado positivo, en este caso, tu probabilidad de tener la enfermedad es de 99 en 10.098, o poco menos del 1%. Sin el enfoque bayensiano se asustaría a muchas personas y se las enviaría a procedimientos médicos intrusivos y potencialmente peligrosos por un diagnóstico erróneo.
Sin conocer la probabilidad previa, no se sabe cuán probable es que un resultado sea falso o verdadero.

FUENTE DE LA IMAGEN,GETTY IMAGES
"Según Bill Gates, la base del éxito de Microsoft fue el uso de Bayes", cuenta McGrayne.
Este no es un problema hipotético.
En medicina, por ejemplo, una revisión de casos realizada en 2016 encontró que el 60% de las mujeres que se hicieron mamografías anuales durante 10 años tuvieron al menos un falso positivo. En los tribunales de justicia, una falla conocida como la "falacia del fiscal", que puede condenar a inocentes, también depende del teorema.
Y eso es sólo la punta del iceberg. Los investigadores utilizan la estadística bayesiana para abordar problemas de formidable complejidad.
El razonamiento bayesiano combinado con la potencia informática avanzada ha revolucionado la búsqueda de planetas que orbitan estrellas distantes; las estadísticas bayesianas contribuyeron a la reducción de la edad del Universo, que a fines de la década de 1990 se calculaba entre 8.000 a 15.000 millones de años y ahora se ha concluido con cierta confianza que es de 13.800 millones de años.
"Hoy en día se utiliza en la genética, para detectar diferencias sutiles en el ADN y las proteínas, así como para proteger la vida silvestre, hacer estudios cerebrales, traducir idiomas extranjeros...", enumera la autora de "La teoría que nunca murió".
"Se ha incrustado en la informática, el aprendizaje automático, la inteligencia artificial.
"Puede que no sea exactamente como lo hizo Bayes, pero se ha modernizado y es increíblemente útil... está en todas partes", señaló McGrayne en conversación con la BBC y concluyó con una cita que se le han atribuido a los economistas John Maynard Keynes y Paul Samuelson, así como al premier británico Winston Churchill y otros, para resumir la esencia del teorema de Bayes:
"Cuando los hechos cambian, yo cambio de opinión. ¿Usted qué hace?".
Feria de Proyectos 2018 II
Feria de Proyectos 2018 II Desarrollando la creatividad y la innovación para la solución de problemas y necesidades del país a tr...




